Ausflug der 4B ins math.space zu einem Vortrag von Prof. Dr. Rudolf Taschner:
Ausflug der 4B ins math.space zu einem Vortrag von Prof. Dr. Rudolf Taschner:
Zu Beginn des Vortrags erläuterte der Professor die unterschiedlichen mythologischen Weltanschauungen der Griechen im Gegensatz zu den Ägyptern und Mesopotamiern. Dann beschrieb er uns den Werdegang des Pythagoras. Wie er vor ca. 2500 Jahren in Samos geboren wurde, dort seine Ausbildung genoss und dann zuerst nach Ägypten, dann nach Babylon, nach Mesopotamien und später dann auch nach Kleinasien reiste, wo er in Milet in dem berühmten griechischen Philosophen Thales von Milet einen Mentor fand. Nun erzählte der Professor ein wenig über Thales von Milet und dessen Ideen. Unter anderem erklärte er die Weltsicht des Thales, alles bestünde aus Wasser. Der erste Höhepunkt des Vortrages war der Beweis des Satzes von Thales.
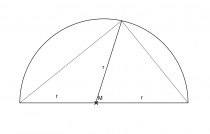
Dazu betrachtete der Herr Professor zunächst einen Halbkreis, in dem ein Dreieck liegt.
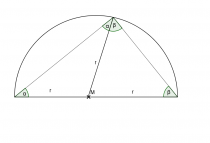
Nun hat das linke Teildreieck offensichtlich zwei gleich lange Schenkel, da sie beide dem Radius des Kreises entsprechen. Doch dasselbe Argument lässt sich auch auf das rechte Teildreieck verwenden. Wenn man nun Winkel einzeichnet, kann man schon einiges erkennen.
Wenn man nun wieder das große Dreieck betrachtet, kann man mit der Information, dass die Winkelsumme eines Dreiecks 180° ergibt (was in späterer Folge noch gezeigt wird), leicht folgende Gleichung aufstellen:
2α + 2β = 180°
Teilt man diese Gleichung nun durch 2, kommen wir auf:
α + β = 90°
Und siehe da, der Winkel im Halbkreis ist genau α + β. Daraus folgt nun, dass der Winkel im Halbkreis immer 90° besitzt. Danach widmete sich der Professor dem Beweis, dass die Winkelsumme eines Dreiecks 180° ergibt.
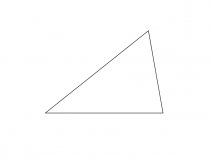
Dazu wählte er als erstes ein beliebiges Dreieck:
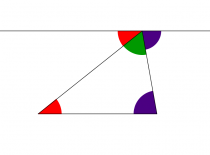
Wenn man eine Parallele zu der Grundfläche zieht und einige Parallelwinkel einzeichnet, kommt man auf folgende Zeichnung:
Hier erkennt man sehr gut, dass folgende Formel Gültigkeit besitzen muss:
blau + rot + grün = 180°
Und die drei Winkel im Dreieck haben genau die Größen rot, blau und grün, also eine Winkelsumme von 180°.
Bei diesen Beweisen unterstrich der Herr Professor deutlich die allgemeine Gültigkeit des mathematischen Beweises. Man kann bei noch so vielen Dreiecken die Winkelsumme messen, man wird sich aufgrund der unendlichen Anzahl an möglichen Dreiecken und der nicht zu vermeidenden Messungenauigkeit nie sicher sein können, dass es nicht irgendein Dreieck gibt, bei dem die Winkelsumme nicht 180° ergibt. Erst durch den mathematischen Beweis ist allgemeine Gültigkeit gegeben.
Nach diesen Ausführungen kam der Professor auf die Pythagoreer zu sprechen, diese Gruppe von „Wissenden“, wie der Professor sie nannte, die Angehörigen der Schule, die Pythagoras gegründet hatte. Er erzählte uns auch von der Vorstellung der Pythagoreer, eine Technokratie mit ihnen an der Spitze aufzubauen. Außerdem berichtete er von den vergeblichen Versuchen der Pythagoreer, sich zuerst auf der Insel Kreta und dann in der italienischen Stadt Kroton zu Herrschern aufzuschwingen.
Später dann gaben sich die Pythagoreer mit dem Gründen einer Schule zufrieden und Professor Taschner kam zum Höhepunkt seiner Ausführungen, dem Beweis des Satzes von Pythagoras.
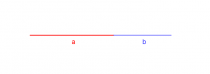
Dazu betrachtete der Professor eine Strecke von der Länge a und eine daran angrenzende Strecke b.
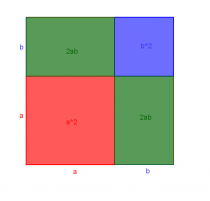
Wenn man nun mit der Seitenlänge a + b ein Quadrat mit dem Flächeninhalt $latex \left( a + b \right)^2 $ zeichnet, erkennt man folgendes:
Hieraus ergibt sich die Gültigkeit folgende Formel:
$latex \left( a + b \right)^2 = a^2 + 2ab + b^2$
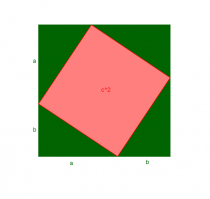
Schlichten wir dieses Viereck nun ein wenig um, kommen wir auf:
Mit dieser Zeichnung können wir nun noch eine zweite Gleichung aufstellen, nämlich:
$latex \left( a + b\right)^2 = c^2 + 2ab$
Wenn man nun die beiden $latex \left( a + b \right)^2 $ gleichsetzt erhält man:
$latex a^2 + 2ab + b^2 = c^2 + 2ab$
Subtrahiert man 2ab auf beiden Seiten, erhält man den allseits bekannten Satz des Pythagoras:
$latex a^2 + b^2 = c^2 $
Gegen Ende des Vortrages erläuterte Professor Taschner, dass es in der heutigen Welt zu einer Neuauflage des Weltbildes von Pythagoras gekommen ist, welches sich in seinem wahrscheinlich bekanntesten Zitat: „Alles ist Zahl“ ausdrückt. Pythagoras betete die Zahlen förmlich an und in der heutigen Welt beten viele Menschen ebenfalls die Zahlen an. Allerdings nicht die Zahlen von Pythagoras, sondern die 0 und die 1. Die Zahlen, die in einem Computer arbeiten, werden heute angebetet. Mit diesen Ausführungen beendete der Professor den Vortrag.
Max Gschwandtner, 4B